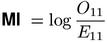
| <<< Previous Section [6] | Back to Contents | [8] Next Section >>> |
while measures in Section 5 gave explicit, intuitively sensible definitions for coeff of ass st, the measures in this section are motivated by the information-theoretic concept of mutual information (MI); there are two variants of MI: pointwise MI measures the amount of overlap between two events, while average MI is a measure of how much information one random variable provides about another, and vice versa; both concepts are defined in terms of theoretical probabilites, i.e. they belong to the parameter space; equations for association measures are obtained by inserting maximum-likelihood estimates for the relevant probabilities
Pointwise MI can be used to measure the "overlap" between occurrences of u and v when it is applied to the corresponding events {U = u} and {V = v}. This results in the mu-value coefficient μ, so the association measure derived from pointwise MI is identical to the MI measure introduced in Section 5.
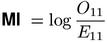
Average MI can be applied to the random variables U and V, in which case its value indicates how much information the components of word pairs provide about each other, averaged over all pair types in the population. The local-MI formula below corresponds to the contribution of the chosen pair type (u,v) to the total average MI of the population. Heuristically, it scales the MI measure with the cooccurrence frequency O11 as a rough indicator of the amount of evidence provided by the sample. It is also interesting to compare local-MI with the almost identical Poisson-Stirling measure.(1)
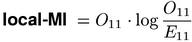
Average MI can also be applied to the indicator variables I[U=u] and I[V=v], which define the contingency table of a pair type (u,v). This leads to the average-MI association measure. Note that local-MI corresponds to the (usually dominant) first term in the summation below.
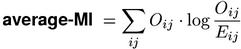
Astonishingly, the average-MI measure is identical to the test statistic of the likelihood ratio test (log-likelihood). Thus, the information-theoreticapproach described in this section has not led to any genuinely new measures, but provides further motivation and theoretical support for three existing measures (MI, Poisson-Stirling, and log-likelihood).
| <<< Previous Section [6] | Back to Contents | [8] Next Section >>> |