8   Heuristic measures

This section contains a final set of association measures, for which no theoretical motivation or derivation can be given. Their equations are founded on purely heuristic arguments or are heuristic variants of other measures. The simplest possible association measure is the plain cooccurrence frequency of the pair types. Its use is motivated by the assumption that associated word pairs will in general occur more frequently than arbitrary combinations, which is related to the recurrence criterion of Firth (1957). In the empirical evaluation of association measures, frequency is often used as a baseline against which the more sophisticated measures are compared (cf. Evert & Krenn, 2001).

The following two measures are heuristic variants of MI, which attempt to reduce its overestimation of low-frequency data by increasing the influence of the cooccurrence frequency O₁₁ in the numerator. It is interesting to compare this heuristic approach with the information-theoretic local-MI measure defined in Section 7, which gives much greater weight to the cooccurrence frequency.

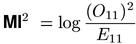
MI² has some theoretical support because it is equivalent to the gmean measure (see Section 5).⁽¹⁾. For the purely heuristic MI³ measure, which was suggested by Daille (1994), there is no such background. Daille considered versions of MI with (O₁₁)^k in the numerator for k = 2 .. 10, obtaining the best performance (in her application) for k = 3.

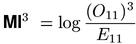
Finally, the random association measure deserves to be mentioned, which uses random numbers as association scores (so no equation can be given for this measure). In a collocation extraction task it corresponds to the baseline of purely random candidate selection. The random measure is also used by the UCS toolkit to break ties in the rankings of other association measures.