6   Conservative estimates of association strength

As has been pointed out in the previous section, the maximum-likelihood estimates for coefficients of association strength do not correct for sampling error, whose effect is greatest for low-frequency data. The MI measure is particularly sensitive to random variation and may substantially overestimate the true association strength (quantified by the mu-value μ). Johnson (2001) suggested to use a confidence interval estimate for μ instead. The lower boundary of this confidence interval then provides a conservative version of the MI measure (which corrects for sampling variation, erring on the side of caution).

The general procedure for obtaining confidence interval estimates is usually based on an exact hypothesis test (cf. Section 3). This test is applied to the observed contingency table, with the null hypothesis of independence (which can be written as H₀: μ = 1) replaced by the hypothesis H_x: μ = x (for an arbitrary value x). When there is enough evidence against H_x, it is rejected at the pre-defined significane level α. The confidence interval estimate for μ is the set of all possible values x for which the corresponding null hypothesis H_x can not be rejected. Since this set includes all values that are not ruled out by the available evidence, the true value of μ should lie somewhere in the confidence interval. The confidence level of the estimate is determined by the complement 1 - α of the significance level (95% confidence for α = .05, 99% confidence for α = .01, etc.).

Johnson based his estimates on the binomial test (i.e. the binomial measure), but in the light of the numerical difficulties pointed out in Section 3, the Poisson approximation is a much better choice. For a given significance level α, the confidence interval of μ consists of all values x for which the p-value of the observed cooccurrence frequency O₁₁ (under a point null hypothesis corresponding to H_x) is greater than or equal to α. A conservative estimate for the MI measure is given by the logarithm of the lower boundary of this interval, leading to the definition shown below.

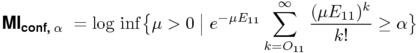
Like the Poisson measure, the sum in the equation of MI_conf,α can be expressed in terms of the incomplete Gamma function (Weisstein, 1999, s.v. Incomplete Gamma Function), and the lower boundary of the confidence interval is easily obtained from its inverse, which is available in some software libraries. Alternatively, the conservative estimate can efficiently be determined by binary search because the incomplete Gamma function is monotonic.

The association scores of MI_conf,α depend on the pre-determined significance level α, which has to be chosen by the researcher. Johnson himself used the uncommon values α = .1 (90% confidence) and α = .0001 (99.99% confidence) in a small evaluation experiment. As he argues in the introduction to (Johnson, 2001), α is a parameter that allows us to make a trade-off between unbiased estimation for high-frequency data and the over-estimation of low-frequency data. Such parametric association measure open up the possibility of optimisation for a specific application (e.g. extracting collocations of a particular type from text corpora).

Johnson (2001) also describes a conservative estimate for the odds-ratio measure, based on a sampling distribution with fixed row and column totals. This distribution depends only on the value of the θ coefficient (Agresti, 1992, p. 134), so H₀ is replaced by the modified null hypothesis H_x: θ = x. The computation of this so-called non-central hypergeometric distribution is numerically expensive. Similar to the Fisher measure, it poses the additional problem that its normalising factor (in the denominator) can only be obtained by explicit summation over all possible values of X₁₁.