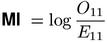
| <<< Previous Section [4] | Back to Contents | [6] Next Section >>> |
The association measures presented in this section belong to the degree of association group. They are maximum-likelihood estimates for various coefficients of association strength (cf. Section 1). As such, all the measures are subject to large sampling errors, especially for low-frequency data. See Section 6 for an attempt to control random variation and avoid inflated association scores.
In Section 1 the two most common coefficients of association strength were introduced, the mu-value μ and the odds ratio θ. Church & Hanks (1990) used the maximum-likelihood estimate for the logarithm of μ as an association measure, which they interpreted (and motivated) as pointwise mutual information (MI), a concept from information theory. This MI measure is particularly prone to overestimate low-frequency data (where E11 is small), but it has nonetheless become a de facto standard in (mainly British) lexicography, often in combination with the t-score measure.
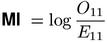
In mathematical statistics, the odds ratio θ is often preferred to μ because of its convenient formal properties (cf. Agresti, 1990, Ch. 2). While the mu-value (and thus the MI score) has an intuitive interpretation (namely, that cooccurrences are μ times more likely than by chance), it is difficult to interpret θ (and thus the odds-ratio measure) in such meaningful terms. Blaheta & Johnson (2001) note that θ is the relevant (association) coefficient of a log-linear model for the 2-by-2 contingency table, which gives the odds-ratio measure some theoretical interest.
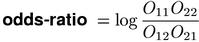
The value of odds-ratio is undefined (or infinite, by continuous extension) when one of the non-diagonal cells has a count of zero (O12 = 0 or O21 = 0). Such infinite or undefined scores can be avoided by a discounting technique, where 0.5 is added to each observed frequency before the ratio is calculated. Discounting also increases the discriminative power of the odds-ratio measure.(1)
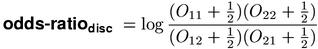
Two other coefficients are less widely used. Relative risk (cf. Agresti, 1990, Ch. 2) is similar to the odds ratio, but is not symmetric between columns and rows (an analogous measure using the row totals instead of the column totals would compute different scores).
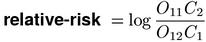
The difference of the column proportions was suggested by Liddell (1976) as a coefficient of association strength. Substitution of maximum-likelihood estimates for the population parameters leads to the equation shown below, which Liddell used as a test statistic.
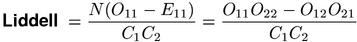
The coefficients of association strength underlying the measures above are closely related to the null hypothesis of independence. They can be derived by "extrapolation" from the condition π = π1 π2. For a non-associated pair, all coefficients (or their logarithms) assume a zero value (although the maximum-likelihood estimates are affected by sampling error, of course). Another group of coefficients are based on the ratios π ⁄ π1 and π ⁄ π2, which are estimated by the proportions O11 ⁄ R1 and O11 ⁄ C1. These coefficients (and the corresponding association measures) are particularly sensitive to strong directional association (where almost every instance of u cooccurs with v or vice versa). On the other hand, they do not assume a fixed value for independent pair types and thus cannot distinguish between positive and negative association.
In order to obtain a single quantitative measure of association strength, the two parameter ratios (or frequency proportions) have to be combined in some way. The following association measures differ in the "link function" used to achieve this combination. Two straightforward choices of a link function, the arithmetic mean and the maximum, have never been used either as a coefficient in mathematical statistics or as an association measure. Pedersen & Bruce (1996) suggest the minimum as a link function, calling their new formula the minimum sensitivity (MS) measure.(2) 30 years earlier, a slight variation of this equation was introduced under the name "rectangular distance" (Kuhns 1965, 35).
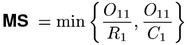
The gmean measure, which uses the geometric mean (Weisstein, 1999, s.v. Geometric Mean) as a link function, is interesting because of its similarity to MI (cf. Section 8). A convenient formal property is that it only depends on the observed and expected joint frequencies.
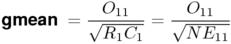
The best-known coefficient from this group is the Dice coefficient, whose link function is the harmonic mean (Weisstein, 1999, s.v. Harmonic Mean). The Dice association measure was used by Smadja (1993) for the extraction of collocations from text corpora. Dias et al. (1999) introduced an extension of Dice to larger N-grams under the name mutual expectation.
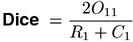
Both the Dice coefficient and the similar Jaccard coefficient have found wide-spread use in the field of information retrieval. The Dice and Jaccard measures are fully equivalent, i.e. there is a monotonic transformation between their scores.(3)
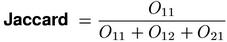
Most of the association measures presented in this section can already be found in a collection by Kuhns (1965). However, his equations replace O11 by the difference O11 - E11, making their interpretation as (functions of) theoretical probabilities problematic.
| <<< Previous Section [4] | Back to Contents | [6] Next Section >>> |