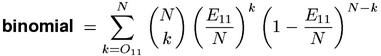
| <<< Previous Section [2] | Back to Contents | [4] Next Section >>> |
While a small likelihood indicates an unusal outcome, its precise value does not have a direct and meaningful interpretation as the amount of evidence against H0, because only a single outcome is considered. Statistical hypothesis tests, on the other hand, compute the total probability of all possible outcomes that are similar to or more "extreme" than the observed contingency table. This total probability is called a p-value. When it falls below a certain threshold, the sample is said to provide significant evidence against the null hypothesis, which is then rejected. Thus, the p-value provides a measure of the amount of evidence against H0, and its negative base 10 logarithm can be used as an association score (note that the equations below compute the non-logarithmic value). All measures in this sections are one-sided, i.e. they will only respond to positive association (while negative association is interpreted as "no evidence" against the null hypothesis).
A fundamental problem in the formulation of a statistical hypothesis test is how to define more "extreme" outcomes. The observed frequencies in a contingency table can vary freely in three dimensions (while the fourth value is determined by the sample size). For this reason, there is no exact hypothesis test corresponding to the multinomial-likelihood measure. When only the joint frequency O11 is considered, though, it is obvious that larger values provide more evidence for a positive association (i.e. one-sided evidence against H0). The binomial and Poisson measures compute the total probability of all possible outcomes where X11 is greater than or equal to the observed value O11. The former is based on the correct binomial distribution of X11, while the latter uses the Poisson approximation.
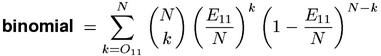
For large sample size N, the formula given above for the binomial measure can become slow and numerically unstable. A more elegant implementation is based on the incomplete Beta function (Weisstein, 1999, s.v. Binomial Distribution), which is provided by various software libraries, but even then the computation is comparatively slow and sometimes inaccurate.
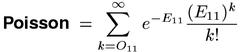
The Poisson measure is not only mathematically more elegant, but also numerically unproblematic. Its implementation can be based on the incomplete Gamma function (Weisstein, 1999, s.v. Incomplete Gamma Function), which is also provided by various software libraries.
The measures above are called exact hypothesis tests because they compute an exact p-value rather than an approximation that is only valid for large samples. However, this terminology glosses over the fact that some uncertainty remains because both tests use the point null hypothesis without taking the sampling error of p1 and p2 into account. Fisher's exact test removes this source of error by conditioning on the observed row and column totals (leading to the hypergeometric sampling distribution of the hypergeometric-likelihood meaure). It can thus be considered a "truly exact" test and is now generally accepted as the most appropriate test for independence in a 2-by-2 contingency table (cf. Yates, 1984).
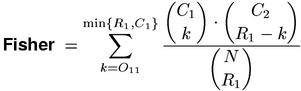
Pedersen (1996) suggested to use the p-value of Fisher's exact test as the Fisher association measure, arguing that it is more accurate than the asymptotic hypothesis tests that had previously been used (cf. Section 4). A direct implementation of the Fisher measure is computationally intensive. Whenever possible, library functions for the underlying hypergeometric distribution should be used. In any case, one must resist the temptation of calculating the complement 1 - P of the actual p-value P by summation over k = 0, ..., O11-1. While this approach can be much faster when O11 is small, it becomes wildly inaccurate for the extremely small p-values that are characteristic of cooccurrence data (P < 10-10). Even some library implementations make this mistake, most notably the R language.(1)
| <<< Previous Section [2] | Back to Contents | [4] Next Section >>> |