2   Likelihood measures

Likelihood measures belong to the significance of association group. They equate the amount of evidence against the null hypothesis of independence with the probability (or likelihood) of the observed cooccurrence frequencies under the null hypothesis. The smaller this probability, the more unusal the observed outcome and, consequently, the more evidence there is against H₀. Most measures in this group are based on the point null hypothesis so that the sampling distribution is uniquely defined. Recall that normally the negative base 10 logarithm of the likelihood is used as an association score, while the equations given below compute the non-logarithmic value. All likelihood measures are two-sided, i.e. high scores may indicate either positive or negative association.

The multinomial-likelihood measure computes the probability of the observed contingency table under the point null hypothesis. This value depends on all four cells of the table.

The joint frequency O₁₁ provides the most direct evidence for the association of a pair type. The binomial-likelihood measure computes the probability of the observed joint frequency regardless of the other cells of the contingency table.⁽¹⁾

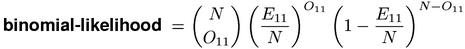
Since the cooccurrence probability E₁₁ ⁄ N under the point null hypothesis is usually small, the binomial distribution of X₁₁ can be approximated by a Poisson distribution, which is both mathematically and numerically more convenient. This leads to the Poisson-likelihood measure.

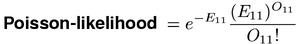
Quasthoff & Wolff (2002) describe an approximation to the negative logarithm of Poisson-likelihood using Stirling's formula. This leads to the Poisson-Stirling measure which has to be scaled appropriately (divide the value shown below by log(10)) in order to allow direct comparison with the other likelihood measures (using the negative-base-10-logarithm convention).

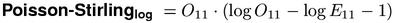
It is possible to avoid the use of maximum-likelihood estimates and the point null hypothesis by conditioning the sampling distribution on the observed row and column totals. The resulting hypergeometric distribution under the general null hypothesis H₀ does not depend on the particular values of the "nuisance" parameters π₁ and π₂. The conditional probability of the observed contingency table defines the hypergeometric-likelihood association measure.

None of the likelihood measures have found widespread use, with the possible exception of Poisson-Stirling,